|
Schachmathematik
|
|
Die Schacholympiade ist der bedeutendste Mannschaftswettbewerb im Schach. Sie wird von der Weltschachorganisation FIDE organisiert und alle zwei Jahre ausgetragen. Zum ersten Mal fand das Turnier offiziell 1927 in London statt. Es spielen Nationalmannschaften an vier Brettern. Anfangs wurde in Vor- und Finalrunden gespielt, seit 1976 nach Schweizer System, bei dem möglichst punktgleiche Mannschaften gegeneinander spielen. Ab 1952 wurde der Wettbewerb von der UdSSR beziehungsweise Russland dominiert, die insgesamt 24 Siege erreichten. Diese Zahl setzt sich aus zwei Serien von zwölf Siegen (1952-1974 und 1980-2002) zusammen, die jeweils mit dem Nichtantreten 1976 und dem Sieg der Ukraine bei der Schacholympiade 2004 in Calvià endeten.
|
Der Spieler mit den meisten Einsätzen bei einer Schacholympiade ist Lajos Portisch, der 20 mal teilnahm und dabei 260 Partien spielte, in denen er 176,5 Punkte erzielte.
Die längste je gespielte Partie an einer Olympiade war ein Remis nach 190 Zügen zwischen Yasser Seirawan und Xu Jun in Thessaloniki 1988.
Die kürzeste Gewinnpartie dauerte nur vier Züge:
1. e2-e4 c7-c5
2. d2-d4 c5xd4
3. Sg1-f3 e7-e5
4. Sf3xe5 Dd8-a5+ Weiß gab auf (Combe – Hasenfuss, Folkestone 1933).
Schachrekorde
Im einem so komplexen und oft gespielten Spiel wie Schach gibt es natürlich auch einige Rekorde
Längste bekannte Mattfolge:
Zwingende Verläufe hin zum Matt können bereits in der Partie recht lang sein; Mattansagen mit über zehn Zügen sind in der Schachgeschichte keine Seltenheit. Bei solchen Mattansagen müssen grundsätzlich auch unsinnig erscheinende Züge berücksichtigt werden, etwa ein Dazwischenstellen eines ungedeckten Steins, der im nächsten Zug geschlagen wird, das Matt aber um einen Zug nach hinten verschiebt.
Komponisten haben sich bereits früh dafür interessiert, wie lang eine zwingende Mattfolge überhaupt sein kann. 1889 veröffentlichte der Ungar Ottó Titusz Bláthy ein Matt in 257 Zügen. Es handelt sich um ein vollwertiges Schachproblem mit dualfreier Hauptvariante (mit Ausnahme des Mattzuges), d.h. im Allgemeinen hat Weiß auf den besten schwarzen Zug immer nur eine optimale Fortsetzung. Dabei ist unterstellt, dass die 50-Züge-Regel nicht gilt. Weiß muss eine lange Zugfolge absolvieren, um ein freies Tempo zu gewinnen, und diese Prozedur dann vielfach wiederholen.
Ganz andere Wurzeln haben andere „Rekordversuche“. Hier geht es um die längsten Endspielmattführungen ohne Rücksicht auf Dualfreiheit und Ästhetik – eine Frage, die schon vor langer Zeit für die Einführung der 50-Züge-Regel entscheidend war. So ist es seit geraumer Zeit gesichertes Wissen, dass das Endspiel von zwei Springern gegen einen Bauern in vielen Stellungen zwingend gewonnen ist, aber bereits vor dem ersten (pattaufhebenden) Bauernzug des Schwarzen über siebzig Züge in Anspruch nehmen kann (wie z.B. der Studienkomponist Alexei Troizki gezeigt hat) oder dass gewonnene Stellungen im Endspiel Turm + Läufer gegen Turm deutlich mehr als 50 Züge bis zum Matt benötigen können.
Durch die vollständige Erfassung sechssteiniger Endspiele in Endspieldatenbanken gelang es zu zeigen, dass das bauernlose Endspiel Turm + Springer gegen zwei Springer in vielen Fällen zwingend gewonnen ist (falls die 50-Züge-Regel nicht gilt). Aufgrund einer von Ken Thompson generierten Datenbank konnte eine KTS/KSS-Stellung etabliert werden, die in nicht weniger als 262 Zügen zum Matt führt.
Längste bekannte Fernpartie:
Die längste bekannte Fernpartie dauerte 16 Jahre. Es handelte sich dabei um eine Partie zwischen Dr. K. Brenzinger aus Pforzheim und F. E. Brenzinger aus New York, die zwischen 1859 und 1875 ausgetragen wurde und nach 50 Zügen mit einem Sieg von Schwarz endete. Im Guinness-Buch der Rekorde von 1971 wird von einer Partie berichtet, die von zwei Spielern aus Schottland und Australien ab 1926 mittels Weihnachtsgrußkarten ausgetragen wurde und zum Zeitpunkt der Veröffentlichung noch andauerte. Die Notation dieser Partie ist allerdings nicht bekannt.
Heute stehen als Übertragungsmittel Fax, E-Mail, SMS oder Schachserver zur Verfügung. So entfällt die Brieflaufzeit, was die Dauer einer Fernpartie erheblich verkürzt. Auf Schachservern wird die Bedenkzeit mittlerweile minutengenau gemessen und die durchschnittliche Partiedauer liegt nicht mehr bei einem Jahr, sondern bei mehreren Monaten.
Kürzeste Mattpartie
Als Narrenmatts bezeichnet man im Schach die kürzestmöglichen Zugfolgen, die von der Ausgangsstellung zum Matt führen. Dies wird z. B. durch folgende Züge erreicht:
1. f2-f3 e7-e6
2. g2-g4 Dd8-h4#
Es gibt acht Zugfolgen, die zu diesem Matt führen: Weißer f-Bauer und schwarzer e-Bauer können jeweils ein oder zwei Felder ziehen, und f- und g-Bauer können die Zugreihenfolge tauschen.
Bei diesem schnellsten Matt ist Schwarz der Mattsetzende, obwohl Weiß den Vorteil des ersten Zuges hat. Der Grund liegt darin, dass der Verlierer bei diesem Matt zwei schlechte Züge ausführen muss. Will Weiß so matt setzen, muss er einen überflüssigen Zug machen. Weil Weiß daran mitwirkt, dem Gegner das schnellstmögliche Matt zu ermöglichen, entspricht das Narrenmatt einem Hilfsmatt.
Weltrekord im Simultanschach
Bein Simultanschach tritt ein Spieler an mehreren Brettern gegen mehrere Gegner gleichzeitig an. Dabei ist der Einzelspieler wesentlich stärker als seine Gegner. Zum Beispiel spielt oft ein Großmeister gegen viele Amateure. Dabei spielt der Simultanspieler in der Regel gegen alle Gegner mit derselben Farbe (meist Weiß). Die Gegner haben immer genau so lange Bedenkzeit, bis der Simultanspieler zum nächsten Zug an ihr Brett tritt, dann müssen sie ziehen.
Die größte Simultanveranstaltung fand am 19. November 1966 in Havanna statt. 380 Schachmeister spielten gegen jeweils 18 Gegner an 6840 Brettern. Wenn eine Simultanveranstaltung mit begrenzter Bedenkzeit ausgetragen wird, spricht man vom Handicap-Simultan. Der Weltrekord im Simultanschach wird seit Februar 2009 von Kiril Georgiew mit 360 Partien gehalten
Späteste Rochade, Rochade mit den wenigsten Steinen und meiste Rochaden
Den Titel der nach Zügen am spätesten erfolgten Rochade halten gleichermaßen die beiden Partien Neshewat–Garrison, Detroit 1994, mit 48. ... 0-0 und Somogyi–Black, New York 2002 mit 48. ... 0-0-0. In beiden Fällen gewann Schwarz.
Die Rochade mit der geringsten Anzahl von Steinen auf dem Brett fand in einer Partie Pupols–Myers, Lone Pine 1976, statt, als Weiß im Endspiel 40. 0-0-0 zog, mit nur noch 8 Steinen auf dem Brett. Die Partie endete Remis.
Die größte Anzahl von Rochaden in einer Partie betrug 3 und wurde in einer Partie Heidenfeld–Kerins, Dublin 1973, gespielt. Weiß rochierte illegalerweise zweimal – unbemerkt, aber vergeblich, denn er verlor die Partie.
Die längste je gespielte Partie an einer Olympiade war ein Remis nach 190 Zügen zwischen Yasser Seirawan und Xu Jun in Thessaloniki 1988.
Die kürzeste Gewinnpartie dauerte nur vier Züge:
1. e2-e4 c7-c5
2. d2-d4 c5xd4
3. Sg1-f3 e7-e5
4. Sf3xe5 Dd8-a5+ Weiß gab auf (Combe – Hasenfuss, Folkestone 1933).
Schachrekorde
Im einem so komplexen und oft gespielten Spiel wie Schach gibt es natürlich auch einige Rekorde
Längste bekannte Mattfolge:
Zwingende Verläufe hin zum Matt können bereits in der Partie recht lang sein; Mattansagen mit über zehn Zügen sind in der Schachgeschichte keine Seltenheit. Bei solchen Mattansagen müssen grundsätzlich auch unsinnig erscheinende Züge berücksichtigt werden, etwa ein Dazwischenstellen eines ungedeckten Steins, der im nächsten Zug geschlagen wird, das Matt aber um einen Zug nach hinten verschiebt.
Komponisten haben sich bereits früh dafür interessiert, wie lang eine zwingende Mattfolge überhaupt sein kann. 1889 veröffentlichte der Ungar Ottó Titusz Bláthy ein Matt in 257 Zügen. Es handelt sich um ein vollwertiges Schachproblem mit dualfreier Hauptvariante (mit Ausnahme des Mattzuges), d.h. im Allgemeinen hat Weiß auf den besten schwarzen Zug immer nur eine optimale Fortsetzung. Dabei ist unterstellt, dass die 50-Züge-Regel nicht gilt. Weiß muss eine lange Zugfolge absolvieren, um ein freies Tempo zu gewinnen, und diese Prozedur dann vielfach wiederholen.
Ganz andere Wurzeln haben andere „Rekordversuche“. Hier geht es um die längsten Endspielmattführungen ohne Rücksicht auf Dualfreiheit und Ästhetik – eine Frage, die schon vor langer Zeit für die Einführung der 50-Züge-Regel entscheidend war. So ist es seit geraumer Zeit gesichertes Wissen, dass das Endspiel von zwei Springern gegen einen Bauern in vielen Stellungen zwingend gewonnen ist, aber bereits vor dem ersten (pattaufhebenden) Bauernzug des Schwarzen über siebzig Züge in Anspruch nehmen kann (wie z.B. der Studienkomponist Alexei Troizki gezeigt hat) oder dass gewonnene Stellungen im Endspiel Turm + Läufer gegen Turm deutlich mehr als 50 Züge bis zum Matt benötigen können.
Durch die vollständige Erfassung sechssteiniger Endspiele in Endspieldatenbanken gelang es zu zeigen, dass das bauernlose Endspiel Turm + Springer gegen zwei Springer in vielen Fällen zwingend gewonnen ist (falls die 50-Züge-Regel nicht gilt). Aufgrund einer von Ken Thompson generierten Datenbank konnte eine KTS/KSS-Stellung etabliert werden, die in nicht weniger als 262 Zügen zum Matt führt.
Längste bekannte Fernpartie:
Die längste bekannte Fernpartie dauerte 16 Jahre. Es handelte sich dabei um eine Partie zwischen Dr. K. Brenzinger aus Pforzheim und F. E. Brenzinger aus New York, die zwischen 1859 und 1875 ausgetragen wurde und nach 50 Zügen mit einem Sieg von Schwarz endete. Im Guinness-Buch der Rekorde von 1971 wird von einer Partie berichtet, die von zwei Spielern aus Schottland und Australien ab 1926 mittels Weihnachtsgrußkarten ausgetragen wurde und zum Zeitpunkt der Veröffentlichung noch andauerte. Die Notation dieser Partie ist allerdings nicht bekannt.
Heute stehen als Übertragungsmittel Fax, E-Mail, SMS oder Schachserver zur Verfügung. So entfällt die Brieflaufzeit, was die Dauer einer Fernpartie erheblich verkürzt. Auf Schachservern wird die Bedenkzeit mittlerweile minutengenau gemessen und die durchschnittliche Partiedauer liegt nicht mehr bei einem Jahr, sondern bei mehreren Monaten.
Kürzeste Mattpartie
Als Narrenmatts bezeichnet man im Schach die kürzestmöglichen Zugfolgen, die von der Ausgangsstellung zum Matt führen. Dies wird z. B. durch folgende Züge erreicht:
1. f2-f3 e7-e6
2. g2-g4 Dd8-h4#
Es gibt acht Zugfolgen, die zu diesem Matt führen: Weißer f-Bauer und schwarzer e-Bauer können jeweils ein oder zwei Felder ziehen, und f- und g-Bauer können die Zugreihenfolge tauschen.
Bei diesem schnellsten Matt ist Schwarz der Mattsetzende, obwohl Weiß den Vorteil des ersten Zuges hat. Der Grund liegt darin, dass der Verlierer bei diesem Matt zwei schlechte Züge ausführen muss. Will Weiß so matt setzen, muss er einen überflüssigen Zug machen. Weil Weiß daran mitwirkt, dem Gegner das schnellstmögliche Matt zu ermöglichen, entspricht das Narrenmatt einem Hilfsmatt.
Weltrekord im Simultanschach
Bein Simultanschach tritt ein Spieler an mehreren Brettern gegen mehrere Gegner gleichzeitig an. Dabei ist der Einzelspieler wesentlich stärker als seine Gegner. Zum Beispiel spielt oft ein Großmeister gegen viele Amateure. Dabei spielt der Simultanspieler in der Regel gegen alle Gegner mit derselben Farbe (meist Weiß). Die Gegner haben immer genau so lange Bedenkzeit, bis der Simultanspieler zum nächsten Zug an ihr Brett tritt, dann müssen sie ziehen.
Die größte Simultanveranstaltung fand am 19. November 1966 in Havanna statt. 380 Schachmeister spielten gegen jeweils 18 Gegner an 6840 Brettern. Wenn eine Simultanveranstaltung mit begrenzter Bedenkzeit ausgetragen wird, spricht man vom Handicap-Simultan. Der Weltrekord im Simultanschach wird seit Februar 2009 von Kiril Georgiew mit 360 Partien gehalten
Späteste Rochade, Rochade mit den wenigsten Steinen und meiste Rochaden
Den Titel der nach Zügen am spätesten erfolgten Rochade halten gleichermaßen die beiden Partien Neshewat–Garrison, Detroit 1994, mit 48. ... 0-0 und Somogyi–Black, New York 2002 mit 48. ... 0-0-0. In beiden Fällen gewann Schwarz.
Die Rochade mit der geringsten Anzahl von Steinen auf dem Brett fand in einer Partie Pupols–Myers, Lone Pine 1976, statt, als Weiß im Endspiel 40. 0-0-0 zog, mit nur noch 8 Steinen auf dem Brett. Die Partie endete Remis.
Die größte Anzahl von Rochaden in einer Partie betrug 3 und wurde in einer Partie Heidenfeld–Kerins, Dublin 1973, gespielt. Weiß rochierte illegalerweise zweimal – unbemerkt, aber vergeblich, denn er verlor die Partie.
|
Jüngster Komponist eines veröffentlichten Problems: Zsuzsa Polgár
Zsuzsa (eigentlich Zsuzsanna) Polgár [ˈʒuʒɒ ˈpolgaːr] (* 19. April 1969 in Budapest), oder Susan Polgar, ist eine ungarisch-amerikanische Schachspielerin. Sie gilt als eine der spielstärksten Schachspielerinnen der Geschichte. Zsuzsa Polgár erlernte bereits sehr früh das Schachspiel und wurde, wie ihre jüngeren Schwestern Zsófia und Judit, von ihrem Vater László Polgár trainiert. 1973 gewann sie als Vierjährige die Budapester Mädchenmeisterschaft der Unter-11-Jährigen mit zehn zu null Punkten. Im gleichen Jahr komponierte sie ihr erstes Schachproblem. 1991 wurde ihr der Großmeistertitel vom Weltschachbund FIDE verliehen. 1993 scheiterte sie im Kandidatenturnier gegen die georgische Großmeisterin Nana Iosseliani erst nach Losentscheid. |
Doch von 1996 bis 1999 war sie Schachweltmeisterin. Sie gewann den Titel durch einen Wettkampfsieg mit 8,5-4,5 gegen Xie Jun. Zur Titelverteidigung trat sie nicht an, weil sie gerade Mutter geworden war und eine Terminverlegung beantragt hatte. Der Weltschachbund FIDE akzeptierte diese Forderung nicht und erkannte ihr den Titel ab. In einem Prozess vor dem Internationalen Sportgerichtshof wurden ihr dafür 25.000 US-Dollar Schadensersatz zugesprochen.
Polgár betreibt eine Schachschule (Polgar Chess Center) in New York und gründete 2002 die Susan Polgar Foundation, die sich der Förderung des Jugendschachs widmet. An der Texas Tech University leitet sie seit 2007 das Susan Polgar Institute for Chess Excellence. Sie veröffentlichte mehrere Lehrbücher und -videos über Schach.
Bei der Schacholympiade 2004 in Calvià führte sie das Team der USA zur Silbermedaille und gewann eine Goldmedaille für das beste Einzelergebnis.
Am 1. August 2005 stellte sie in Palm Beach Gardens einen Weltrekord im Simultanschach auf. Sie spielte gleichzeitig gegen 326 Spieler und gewann in 16,5 Stunden 309 Partien bei 3 Niederlagen und 14 Remis. Der Rekord wurde inzwischen von Kiril Georgiew überboten.
Ihre letzte Elo-Zahl stammt aus dem Januar 2005 und beträgt 2577. Seitdem hat sie keine bewertete Partie mehr gespielt
Problemschach
Problemschach ist eine Form der Beschäftigung mit Schach, deren Wurzeln bis zu den Anfängen des Schachspiels zurückreichen. Sie hat sich in den letzten hundertfünfzig Jahren durch Spezialisierung weitgehend verselbständigt. Mitunter wird von Kunstschach gesprochen, um die ästhetische Seite der Schachkomposition zu unterstreichen.
Eine Schachkomposition besteht gewöhnlich aus einer Schachstellung (meist als Diagramm dargestellt), einer Forderung (zum Beispiel „Weiss zieht und gewinnt“) und der Lösung der Aufgabe.
Schachkompositionen werden oft in Schachspalten von Tageszeitungen und Zeitschriften sowie in Schachzeitschriften veröffentlicht. Zudem gibt es Spezialliteratur, die sich ausschliesslich mit Schachkomposition beschäftigt. Falls nicht anders angegeben, richtet sich die Forderung an Weiss, der außer bei Hilfsaufgaben auch am Zuge ist. Für die Lösung gelten im Normalfall die üblichen Schachregeln.
Polgár betreibt eine Schachschule (Polgar Chess Center) in New York und gründete 2002 die Susan Polgar Foundation, die sich der Förderung des Jugendschachs widmet. An der Texas Tech University leitet sie seit 2007 das Susan Polgar Institute for Chess Excellence. Sie veröffentlichte mehrere Lehrbücher und -videos über Schach.
Bei der Schacholympiade 2004 in Calvià führte sie das Team der USA zur Silbermedaille und gewann eine Goldmedaille für das beste Einzelergebnis.
Am 1. August 2005 stellte sie in Palm Beach Gardens einen Weltrekord im Simultanschach auf. Sie spielte gleichzeitig gegen 326 Spieler und gewann in 16,5 Stunden 309 Partien bei 3 Niederlagen und 14 Remis. Der Rekord wurde inzwischen von Kiril Georgiew überboten.
Ihre letzte Elo-Zahl stammt aus dem Januar 2005 und beträgt 2577. Seitdem hat sie keine bewertete Partie mehr gespielt
Problemschach
Problemschach ist eine Form der Beschäftigung mit Schach, deren Wurzeln bis zu den Anfängen des Schachspiels zurückreichen. Sie hat sich in den letzten hundertfünfzig Jahren durch Spezialisierung weitgehend verselbständigt. Mitunter wird von Kunstschach gesprochen, um die ästhetische Seite der Schachkomposition zu unterstreichen.
Eine Schachkomposition besteht gewöhnlich aus einer Schachstellung (meist als Diagramm dargestellt), einer Forderung (zum Beispiel „Weiss zieht und gewinnt“) und der Lösung der Aufgabe.
Schachkompositionen werden oft in Schachspalten von Tageszeitungen und Zeitschriften sowie in Schachzeitschriften veröffentlicht. Zudem gibt es Spezialliteratur, die sich ausschliesslich mit Schachkomposition beschäftigt. Falls nicht anders angegeben, richtet sich die Forderung an Weiss, der außer bei Hilfsaufgaben auch am Zuge ist. Für die Lösung gelten im Normalfall die üblichen Schachregeln.
|
Schachaufgabe des 15. Jahrhunderts im Buch von Lucena
|
Geschichte
Die Schachkomposition ist sehr alt. Schon im arabischen Schach im 10. Jahrhundert gab es Aufgaben („Mansuben“, z. B. das bekannte „Matt der Dilaram“), die aller Wahrscheinlichkeit nach nicht die Erhöhung der Spielstärke, sondern den ästhetischen Genuss von Stellung und Lösung zum Ziel hatten. Im mittelalterlichen Europa waren Mattaufgaben als Gegenstand von Wetten beliebt. In den frühen Schachbüchern des 15. und 16. Jahrhunderts nahmen Schachkompositionen, so in den Werken von Lucena oder Damiano, einen großen Umfang ein. Später behandelte die Schachliteratur dann überwiegend die Eröffnungen und andere Aspekte des praktischen Spiels. Daneben blieb die Tradition der Schachaufgaben erhalten, die im 18. Jahrhundert namentlich der Syrer Philipp Stamma aufgriff. Seit etwa 1830 bildete sich schließlich aus Komponisten und Lösern eine Subkultur der Schachkomposition heraus. Es haben sich in diesem sozialen Netzwerk eine Fülle von Themen und eine eigene Fachsprache entwickelt. Im 19. Jahrhundert entwickelte sich besonders die Schachaufgabe mit der Forderung Matt in n Zügen, auch Schachproblem genannt, zur dominierenden Richtung. |
Aufgaben, die Schach und Mathematik kombinieren
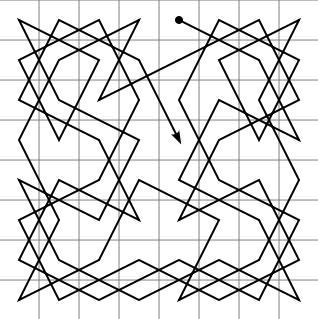
Wege der Figuren auf dem Schachbrett
Wege der Figuren auf dem Schachbrett
Eine typische Aufgabe ist das Springerproblem: Finde einen Weg für den Springer der ihn über das ganze Brett führt, ohne ein Feld zweimal zu betreten. Diese Art von Aufgaben wird auch für verallgemeinerte Schachbretter und für Märchenschachfiguren gestellt.
Aufstellungen von Figuren auf dem Schachbrett
Oftmals geht die Betrachtung von der speziellen Geometrie des Schachbretts aus. Viele Rätselaufgaben handeln davon, Figuren nach festgelegten Bedingungen aufzustellen:
Unabhängigkeit
Wie viele Figuren einer bestimmten Sorte lassen sich auf das Schachbrett stellen, sodass keine im Wirkungsbereich einer anderen steht, und wie viele Möglichkeiten gibt es für eine solche Aufstellung? Die bekannteste derartige Aufgabenstellung ist das vom bayerischen Schachmeister Max Bezzel erdachte Damenproblem.